Section 3.3 Permutations
When counting various outcomes the order of things sometimes matters. When the order of a set of elements changes we call the second a permutation (or an arrangement) of the first.
Notice that if n=1, then there is only 1 item to arrange and that there is only one possible arrangment.
By induction, assume that any set with n elements has n! arrangments and assume that
\begin{gather*}
A = \left \{ a_1, a_2, ... , a_n, a_{n+1} \right \}.
\end{gather*}
Notice that there are n+1 ways to choose 1 element from A and that in doing so leaves a set with n elements. Combining the induction hypothesis with the multiplication principle this gives (n+1)n! = (n+1)! possible outcomes.
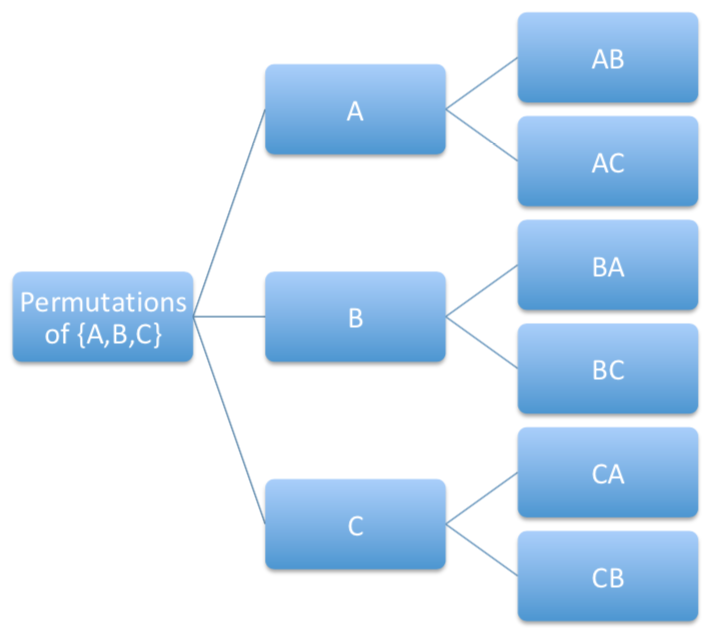
One can interpret successive ordered selections as branching through a "tree" structure. Indeed, starting with the set {A,B,C} one may pick any of the three but then a subsequent selection only has two possibilities for the next selection and so forth. The tree below illustrates that there are six ways to order two items from a group of size three.
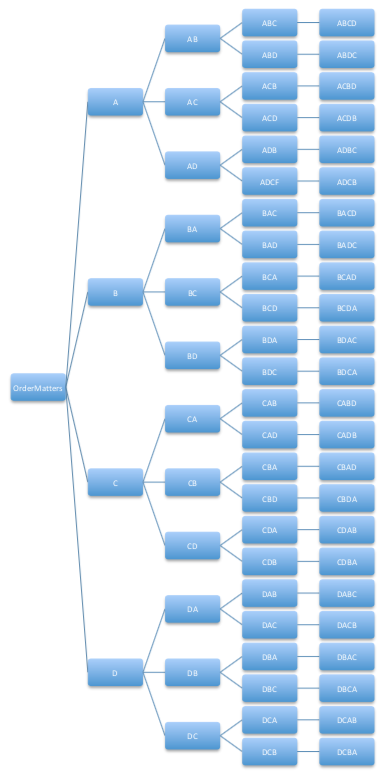
Going one step further, what about ordering the letters in {A, B, C, D}? You can start by picking one of the four letters, say A, and then arranging B, C, and D. Then, start with B and arrange A, C, and D and so on. This gives:
ABCD, ABDC, ACBD, ACDB, ADBC, ADCB
BACD, BADC, BCAD, BCAB, BDAC, BDCA
CBAD, CBDA, CABD, CADB, CDBA, CDAB
DBCA, DBAC, DCBA, DCAB, DABC, DACB
which is 24 different options or \(4! = 4 \cdot 3 \cdot 2 \cdot 1 = 24\text{.}\) This can be viewed using a tree structure where each decision creates a new branch.
The number of ways to arrange r items from a set of n distinct items is This is sometimes denoted also as P(n,r) or \(P_r^n\text{.}\)
Theorem 3.3.2 Permutations of a subset without replacement
\begin{equation*}
_nP_r = \frac{n!}{(n-r)!}
\end{equation*}
Proof
If \(r \gt n\) or \(r \lt 0 \) then this is not possible and so the result would be no permuatations. Otherwise, apply the multiplication principle r times noting that there are n choices for the first selection, n-1 choices for the second selection, and with n-r+1 choices for the rth selection. This gives
\begin{align*}
_nP_r & = n(n-1) ... (n-r+1)\\
& = n(n-1) ... (n-r+1)\frac{(n-r)!}{(n-r)!}\\
& = \frac{n(n-1) ... (n-r+1)(n-r)!}{(n-r)!}\\
& = \frac{n!}{(n-r)!}
\end{align*}
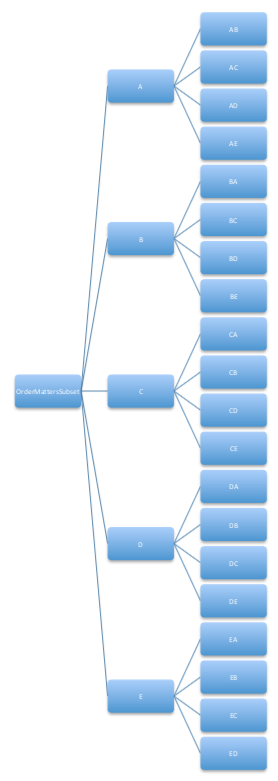
Following the tree idea from above, continue for several steps but then stop once you have gone r steps in. For example, it is easy to see that \(_5P_2 = 20\) using a tree.
Let's apply the the Permutation formula.
So, these are simple calculations.
Theorem 3.3.4 Permutations of a subset with replacement
The number of ways to obtain an arrangement of r choices from a group of size n is
\begin{equation*}
n^r
\end{equation*}
Proof
Use the multiplication principle r times and see that for each choice all n objects in the universe remain available. That is,
\begin{equation*}
n \cdot n \cdot n ... n = n^r
\end{equation*}
Theorem 3.3.5 Permutations when not all items are distinguishable (Multinomial Coefficients)
If n items belong to s categories, \(n_1\) in first, \(n_2\) in second, ... , \(n_s\) in the last, the number of ways to pick all is
\begin{equation*}
\frac{n!}{n_1! \cdot n_2! ... n_s!}
\end{equation*}
Proof
Enumerate all of the n data items individually with the \(n_1!\) identical values first and the remaining groups in like manner to get the enumerated list
\begin{equation*}
\left { x_{1,1}, ..., x_{1,n_1}, x_{2,1}, ..., x_{2,n_2}, ... , x_{s,1}, ..., x_{s,n_2}, \right }
\end{equation*}
In this order, there are \(n_1!\) ways to arrange the first group, \(n_2!\) ways to arrange the second, etc. There are \(n_1! \times n_2! \times ... \times \n_s!\) ways to arrange all of the categories together with groups in this order but none of those group reorders does anything since those data values are all the same. Dividing out those from the \(n!\) original permutations of all items leaves one with the multinomial coefficient.
Let's apply the this new Permutation formula.
Another one bites the dust.