• Finite Precision Machines -- round-off errors. (Computer arithmetic is not exact. A finite mantissa and exponent give rise to only a small subset of rational numbers are expressible on a computer.)

• Approximate mathematical models -- truncation errors. (Finite means of approximating continuous or unknown quantities.)

• Convergence - Stopping an iterative process before completed. (Can't let a process complete an infinite number of steps. Models may asymptotically converge. On a machine, one may only implement a finite number of steps in such a procedure. Hence, stopping before convergence yields an error.

Goal: To produce reasonably accurate results in the presence of (1), (2) and (3) above.

Roundoff Errors

• machine numbers y = ±0.d₁d₂...d_k *bⁿ, where
• b = base of machine,
• n=#of digits in exponent,
• k=#of digits in mantissa,
• d_j = jth digit, such that d₁ is nonzero.
• underflow 0 < |y| < 0.1 * b^minimum, overflow |y| > 1 * b^maximum.
• Notice that combining integer data using addition, subtraction or multiplication will always yields exact results except in the case that overflow is reached.
  
• The set of machine numbers is a very small subset of the rational numbers. For an actual real number x = ±0.d₁d₂...d_kd_k+1 ... bⁿ, the computer can only represent the "closest" machine number, denoted by fl(x).
• Chopping yields fl(x) = first k digits of x, regardless of the (k+1)^st digit
• Rounding yields fl(x) =chopped (x + 0.5 b^k).
• Absolute error.  If p = exact, p* = approx. yields absolute error = | p - p*|. For computer calculations, |x - fl(x)| = 0.d_k+1 ... b^n-k.
• Relative error - generally a better estimate of how bad an approximation really is. | p - p* | / | p |
• Significant digits - number of decimal places which are known to be accurate

• Differencing nearly equal quantities - significant digits may cancel leaving an answer with fewer significant digits.
• Multiplying by large quantities - significant digits might double so that machine number can't maintain all of them.
• Dividing by small quantities - similar to (2).

Ex. Consider quadratic formula in various forms. Notice, mathematically each method is equivalent.
 

Remark: Rounding errors introduce errors in repeated calculations in the same way that incorrect data does.
 

Stability: Small changes in the "initial" data yields correspondingly small changes in the final result.
 

Ex: x_n=(2/3)ⁿ, n>0 found recursively by one of the four methods:

(a) p_n= (2/3)p_n-1, which is a stable algorithm, with the relative error "err_p" virtually zero

(b) q_n= (7/6)q_n-1 - (1/3)q_n-2, which is stable, with the relative error "err_q" the next best, only increasing linearly.  Note, the recursion above also has as a solution (1/2)ⁿ, where 1/2 < 2/3.

(c) r_n= (17/12)r_n-1 - (1/2)r_n-2, which is "relatively" stable, with the relative error "err_r" increasing exponentially.  Note, the recursion above also has as a solution (3/4)ⁿ, where 3/4 > 2/3, but where both solutions still approach zero.

(d) s_n= (8/3)s_n-1 - (4/3)s_n-2, which is unstable, with the relative error "err_s" increasing exponentially at the greatest rate.  Note, the recursion above also has as a solution (2)ⁿ, where not only is 2 > 2/3, but the other solution increases as n increases.

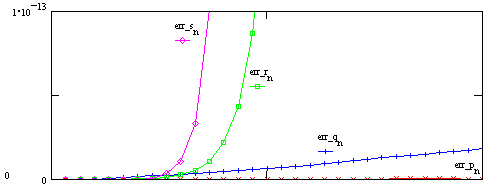
This illustrates the effect of roundoff creeping into a calculation.  As successive terms are calculated, roundoff error allows the "other solution" to enter the mix and the computed solution has some of the characteristics of this other solution as well.  Dependent upon how the "other solution" compares to the desired one shows how the relative error will grow.

Another example of roundoff:  Given x>1, consider the following procedure:

• Repeat x <- sqrt(x) n times
• Then, repeat x <- x² n times

HOMEWORK ASSIGNMENT

COMPUTING ASSIGNMENT

READING ASSIGNMENT
 

Mathematical Problems to Investigate:

1. Finding Roots of equations -- Numerical solution of non-linear equations.

2. Evaluating and Graphing Functions -- Approximation of functions.

3. Integrating Hard Integrals -- Numerical Integration.

4. Finding Hard Derivatives -- Numerical Differentiation

5. Solving Linear Systems of Equations -- Gauss Elimination, Cholesky Factorization, Iterative Methods.

6. Solving Differential Equations -- Numerical O.D.E.s and P.D.E.s.
 

Remark: T is an operator if it maps functions onto other functions. Suppose x and y are functions with T(x)=y. Then we can classify many mathematical problems into one of the following categories:

(a) Direct Problem: Given f and x, find y. (3),(4)

(b) Inversion Problem: Given f and y, find x. (5),(6)

(c) Identification Problem: Given x and y, find f. (2)
 

Types of errors in computational problems:

1. Roundoff Errors - errors from the use of computer generated approximations to non-machine numbers

2. Truncation Errors - errors from the use of discrete mathematical models to approximate continuous or "limiting" problems

3. Convergence Errors - errors from stopping a convergent sequence after a finite number of steps